Bayesian Probability
1 Logic Analogy
\[P(B | A) \cdot P(A) = P(A \land B)\]
Logically the greatest fix point
\[ A \Rightarrow B, A \vdash A \land B \]
| \(P(B | A)\) | \(P(A)\) | \(=\) | \(P(A \land B)\) |
|---|---|---|---|
| \(A \Rightarrow B\) | \(A\) | \(\vdash\) | \(A \land B\) |
2 Developer Analogy
One can see conditional probabilities in terms of states
- State 1: \(P(A)\) [prior]
- State 2: \(P(A | B)\)
- State 3: \(P(A | B C)\)
- State 4. \(P(A | B C ...)\)
We call State 1 our prior and the
conditional probability or final state post-erior
3 Conditional Probability and statistical Alpha
http://www.columbia.edu/~cjd11/charles_dimaggio/DIRE/styled-4/code-12/
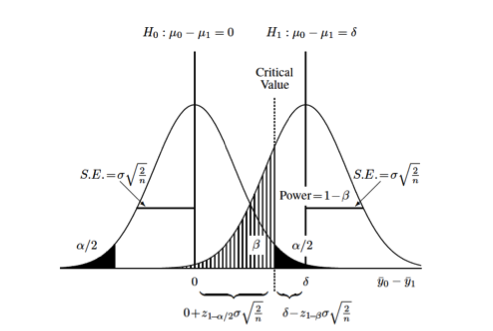
Eg. We run a t-test between 2 sample populations. This returns 2 normal curves with one mean 0, and the other delta representing the DIFFERENCE between populations.
WARNING: The normal curves DO NOT represent each of the 2 sample populations
Type 1 or alpha: P(t-test tells us there is difference | Reality there is no difference)
Type 2 or beta: P(t-test tells us there is no difference | Reality there is a difference)
Power or (1-beta): P(t-test tells us there is a difference | Reality there is a difference) # My Interpretation
Shaded node \(P(A)\) behaves like existential intro
- \(P(A | B)\) shows a relation between partitions of A and B.
- Behaves like function or Implication that is only activated when an object A is given.
- \(P(A)P(A | B)\) merges the partitions A and B together.
4 Misconceptions
Multiplying 2 priors \(P(A)P(B)\) typically is a dead end.
We need the conditional probability to understand the relationship between 2 priors
\[P(A)P(B) \neq P(A\land B)\]
We cannot Overshoot the prior condition of the conditional probability.
Example is fueling \(P(B|A)\) with \(P(A \land C)\) which overshoots the condition of requiring only \(P(A)\). WRONG!
5 Another logic example
\[P(B|A)P(A) + P(B| \lnot A)P(\lnot A)\] \[ (A \land B) \lor (A \land \lnot B) \vdash A \]
5.1 Chain rule
\[\begin{aligned} P(A \land B \land C \land D) &= P(A | B \land C \land D) \cdot P(B \land C \land D) \\ &= P(A | B \land C \land D) \cdot P(B | C \land D) \cdot P(C \land D) \\ &= P(A | B \land C \land D) \cdot P(B | C \land D) \cdot P(C | D) \cdot P(D) \end{aligned}\]
All nodes are called priors. The bridge between nodes are called conditional probabilites.
Question: We want to know what the probability that a set of events happen simultaneously. Given that we know all possible transitions or conditionals.
Answer:
Say we have n nodes(events).
Partition n nodes to 1 and […n-1] nodes. We can find the P(n) = P(A| …n-1)P(…n-1)
What if we don’t know the probability of the […n-1] nodes,
PARTITION n-1 nodes to 1 and […n-2] nodes. …
Know this is only easy if we know all the conditional probabilities before hand.
Prove \(P(A | B \land C ) \cdot P(B | C) = P(B | A \land C) \cdot P(A | C)\)