Lean 3 (archive)

Posted on August 2, 2019
Tags: lean
Logic Intro Elim
\(\rightarrow\) intro intros apply have h_3 := h_1 h_2
\(\forall\) intro intros apply specialize have h_2 := h_1 t
\(\exists\) use cases
\(\lnot\) intro intros apply contradiction
\(\land\) split cases h.1 h.2 h.left h.right
\(\leftrightarrow\) split cases h.1 h.2 h.mp h.mpr rw
\(\lor\) left right cases
\(\bot\) N/A contradiction ex_falso
\(\top\) trivial N/A

Classical logic open_locale classical use by_contradiction tactic

Most of the time, implication and universal quantifier are treated the same.

1 rw

1.1 Example

expected type:
abcd: ℝ
h₁: a ≤ b
h₂: c ≤ d
⊢ ∀ {α : Type u_1} {a b c d : α} [_inst_1 : preorder α] 
[_inst_2 : has_add α] 
[_inst_3 : covariant_class α α (function.swap has_add.add) has_le.le] 
[_inst_4 : covariant_class α α has_add.add has_le.le]
, a ≤ b → c ≤ d → a + c ≤ b + d

Type

For any type α that has a pre order.

2 Types

if p : Prop then x:p is a proof of proposition p : Prop. if y:p is also a proof then proof irrelevance means x:p and y:p are indistinguishable.

3 Numbers

Proofs of numbers typically use type coercion.

norm_num

4 Inductive type

inductive mynat
| zero : mynat
| succ (n : mynat) : mynat

5 Definitional Equality and Reduction

Given
\(A \overset{reduces}{\rightarrow} X\)
\(B \overset{reduces}{\rightarrow} X\)
Implies
\(A \underset{def}{\equiv} B\)
Conversion Definition Example
alpha renaming \(\lambda x. P x \equiv \lambda y. P y\)
beta computing \((\lambda x. x + 2) 3 \equiv 3 + 2\)

6 Dependent type

6.1 Inspiring the dependent type

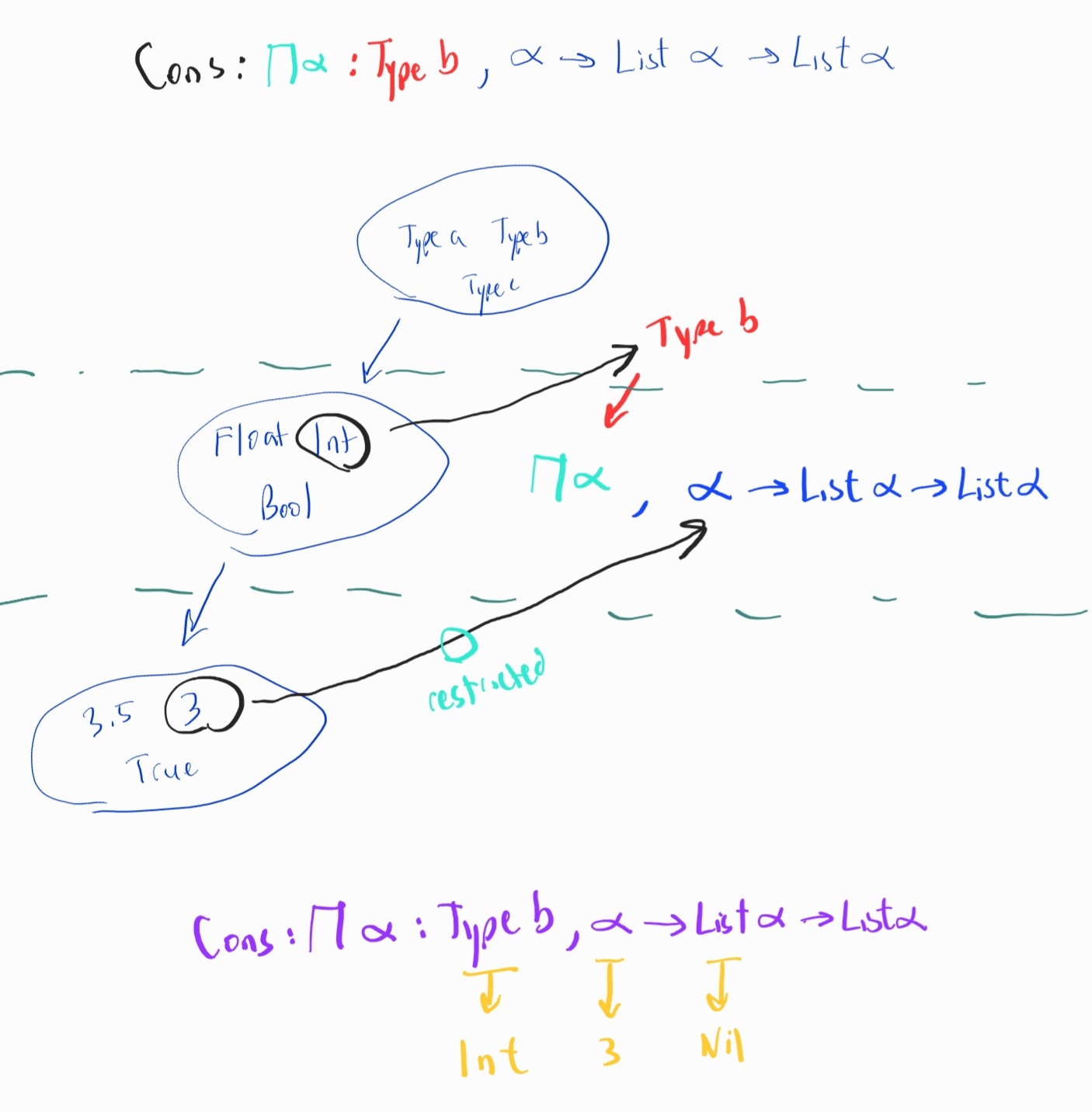
cons 2 [3,4] : List Nat
cons : Nat -> List Nat -> List Nat

What if we wanted a polymorphic cons?
Give first argument as the Type
cons Nat 2 [3,4] : Type -> T -> List T -> List T

  • Nat : Type
  • 2 : T
  • [3,4] : List T

Notice T = Nat

We need T in Type-Space to relate to Nat in Term-Space. How?
Abstract away the term Nat to a bound term variable Π T
Type -> T -> List T -> List T =>
Π T : Type -> T -> List T -> List T

namespace hidden

universe u

constant list   : Type u → Type u

constant cons   : Π α : Type u, α → list α → list α
constant nil    : Π α : Type u, list α
constant head   : Π α : Type u, list α → α
constant tail   : Π α : Type u, list α → list α
constant append : Π α : Type u, list α → list α → list α

#check cons α a (nil α)

end hidden

Observe how we can use Dependent Product Type for polymorphism.

\[\prod_{x: \alpha} \beta = \prod_{x: \alpha} (x \rightarrow list\ x \rightarrow list\ x)\]

Pi-type or dependent product type behaves like lambda in the type space

β is an EXPRESSION that can be expanded.
β may or may not include bound variable x in it’s expression

cons :: Π x : α, β
What is the type of cons int?
We apply (Π x : α, β) to int in the type space.
cons int :: (Π x : α, β)(int)

  1. (Π x : α, β)(int)
  2. Beta-reduction: β[int/x]
  3. β expanded is x -> list x -> list x
  4. β[int/x] is (x -> list x -> list x)[int/x]
  5. replace x with int resulting in
    (int -> list int -> list int)

cons int :: (Π x : α, β)(int) is
cons int :: int -> list int -> list int

Example of a list is cons int 3 (nil int)

Since cons and nil are dependent types, they must take an extra parameter [in this case] int

f :: Π x : α, β = f x :: β[x] where x :: α

6.1.1 function type is just a Pi-type

when β expanded expression does not include
bound variable Π x : α then
β[x] = β

example: f :: Π x : α, β = f x :: β[x] = f x :: β = f :: α -> β

example β is bool, α is nat
Notice bool is an expression that does not include any bound variable x:nat

  • even :: Π x : α, β
  • even :: Π x : nat, bool
  • even :: nat -> bool

6.2 Sigma Type

def f (α : Type) (β : α → Type) (a : α) (b : β a) : (a : α) × β a :=
  ⟨a, b⟩
def h1 (x : Nat) : Nat :=
  (f Type (fun p => p) Nat x).2

-- (α : Type) is (Type : Type)
-- β is (fun p => p : Type -> Type)
-- (a : α) is (Nat : Type)
-- (b : β a) is (x : (fun p => p)(Nat)) which is (x : Nat)

How to look at f? Extract the types
Type -> (α → Type) -> α -> β a -> ((a : α) × β a)

7 Notation

7.1 Curly vs Smooth Parenthesis

  • Curly {a: Type u} stands for notational shortcuts aka implicit arguments that do not need to be written
  • Smooth (a: Type u) stands for explicit aka we need to write out the type as an argument
---- Curly vs Bracket
---- {a: Type u} vs (a: Type u)
---- implicit argument vs explicit

--They mean the same but implicit argument allows us to omit arguments for shorter declarations.

--implicit argument means that {a: Type u} will get autofilled
-- ex1: "nil nat" becomes "nil", the "nat" is the implicit argument that gets autofilled
-- ex2: "cons nat 4 (nil nat)" becomes "cons 4 nil", here we see {a: Type u} is "nat"
--

variables p : list nat 
universe u
--implicit arguments are just notation shortcuts
constant consImplicit {a : Type u } :  a -> list a -> list a 
constant nilImplicit : Π {a : Type u}, list a
#check consImplicit --?M_1 → list ?M_1 → list ?M_1 
--consA shows metavar like ?M_1

--using @ fills in the metavar with types
#check @consImplicit

#check nilImplicit 
#check consImplicit 4 nilImplicit  

--explicit arguments

constant consExplicit (a : Type u) : a -> list a -> list a

constant nilExplicit : Π (a : Type u), list a
#check consExplicit
#check consExplicit
#check consExplicit 4 nilExplicit --error
#check consExplicit 4 nilExplicit --error

#check consExplicit nat 4 (nilExplicit nat) --ok

7.2 Pi-type, forall, parenthesis

-- notice that we Pi-type == forall or we can push the quantifier into a parenthesis. 
-- three cons below are the same.
constant consA :  Πa  : Type u , a -> list a -> list a
constant consB : ∀a  : Type u , a -> list a -> list a
constant consC : ∀(a : Type u), a -> list a -> list a 
constant consD : Π(a : Type u) , a -> list a -> list a
constant consE (a : Type u) : a -> list a -> list a

8 Simple interpreter

section basiclang

inductive Term : Type 
| T : Term 
| F : Term 
| O : Term 
| IfThenElse : Term -> Term -> Term -> Term 
| S : Term -> Term 
| P : Term -> Term 
| IsZero : Term -> Term

open Term

def eval : Term -> Term
| (IfThenElse T s2 s3) := s2 
| (IfThenElse F s2 s3) := s3
| (IfThenElse s1 s2 s3) := 
  let ns1 := eval s1 in (IfThenElse ns1 s1 s2) 
| (S s1) := 
  let ns1 := eval s1 in (S ns1)
| (P O) := O
| (P (S k)) := k 
| (P s1) := 
  let ns1 := eval s1 in (P ns1)
| (IsZero O) := T 
| (IsZero (S k)) := F 
| (IsZero s1) :=
  let ns1 := eval s1 in (IsZero ns1)
| _ := F

#reduce eval $ P $ S $ P O
#reduce eval $ IsZero O
#reduce eval $ IfThenElse (IsZero O) (S O) (S $ S O)
---  s1 -> ns1
--- ---------------
---  S s1 -> S ns1

def ToNat : Term -> nat 
| O := 0 
| (S (n: Term)) := 1 + ToNat n 
| _ := 1

#reduce ToNat (eval $ S $ S $ S $ O)
end basiclang

--extensionality vs intensionality
--extensionality means functions that behave the same are the same
--intensionality means functions that behave the same but built differently are not the same

def foo : ℕ → ℕ → ℕ
| 0     n     := 0
| (m+1) 0     := 1
| (m+1) (n+1) := 2

#reduce foo 5 0


section Combinators

def I {a : Type*} : a -> a :=  λx , x
def K {a b: Type*} : a -> b -> a := λx , λy, x
def app {a b: Type*} : (a -> b) -> a -> b := λf, λx, f x 
def S {a b c: Type*} : (a -> b -> c) -> (a -> b) -> a -> c := λf, λg, λa , f a (g a)

#eval I 2
#check S K S K
#check K K (S K)
#check (S I I)
end Combinators

#reduce (λx, x + 2)5

9 Understanding Coq

What below means is that pairn :: nat -> nat -> natprod aka pairn (n1 n2) :: natprod

(* correct version *)
Inductive natprod : Type :=
  | pairn (n1 n2 : nat).

What below means is that pairn :: Π(na : nat) -> Πi(nb : nat) -> nat -> nat -> natprod na nb

Inductive natprod (na nb : nat): Type :=
  | pairn (n1 n2 : nat).
Inductive bleh (one : Type a) : Type := ...

Definition bleh (one: Type a) : Type := ...